悬臂梁
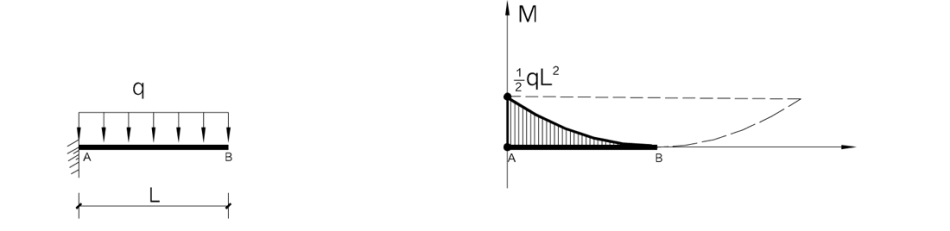
Mx= 1/2q(X-L)²
- 当x=0时,M=1/2qL²
- 当x=L时,M=0
简支梁
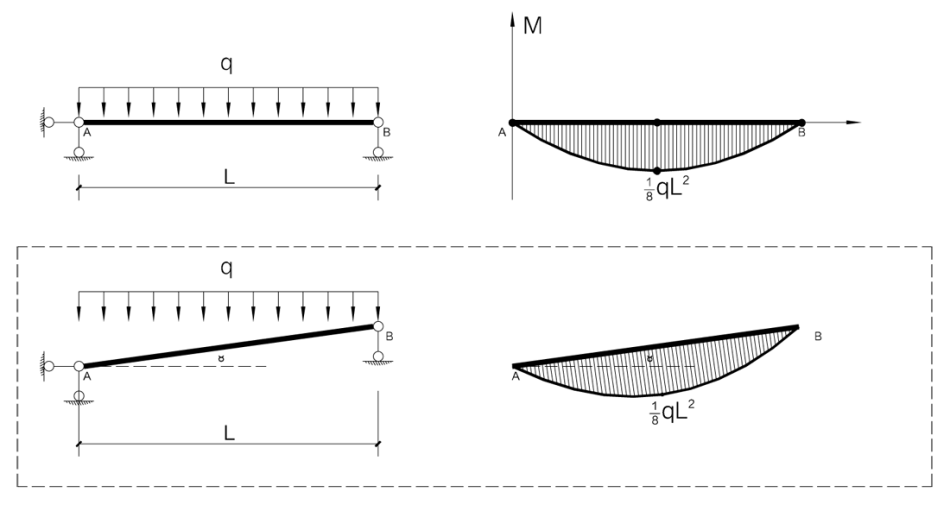
Mx=1/2q(X-1/2L)² -1/8qL²
Mx=1/2q(X-L)(X-0)
- 当X=0或L时,M=0
- 当X=1/2L时,M=1/8qL²
固端梁(两端固定)
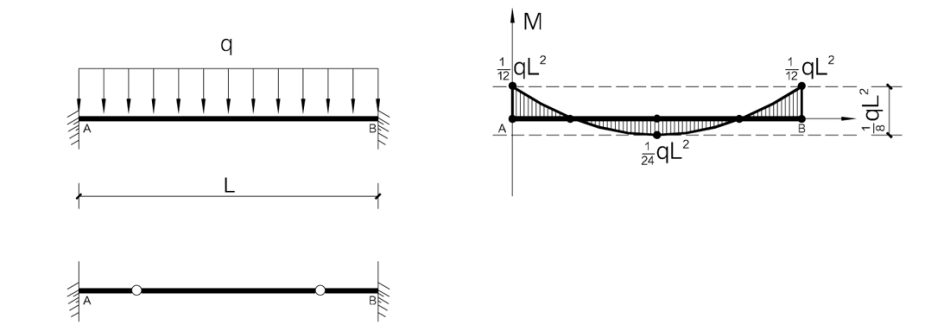
- 当X=(3-√3)/6≈0.21时,M=0
- 端部弯矩 1/12qL²
- 跨中弯矩 1/24qL²
两端固定梁 = 悬臂梁 + 简支梁(1/√3L)
在距端部约 1/√3L 处采用销结合连起来的梁,与未断开过的连续梁的应力和挠度是一样的。也就是说,由于两端固定可看做是由端部的悬臂梁和中央的简支梁组合而成,因此便能够在设计时将两端固定梁分别作为1根简支梁和2根悬臂梁来处理。不过,如果两端固定的可靠程度较差的话,则很危险。
而且,由于我们认为两端固定梁是一种端部和中央部分不同的梁,因此应该考虑把梁、尤其是较长的梁的结合处设计成不同的截面,以确保连接得更加牢固。
端部弯矩 + 跨中弯矩 = 简支梁跨中弯矩
如果把端部弯矩与跨中弯矩的绝对值相加为1/8qL²,结果与简支梁跨中弯矩相同。由此可以引申出以下意义:两端固定梁其实就是一种端部被约束着、并因而使中央弯矩变小的梁。反之,亦可作这样的理解:当两端固定梁的端部约束程度下降时,其中央弯矩必然增大。
固端梁(一端固定,一端简支)
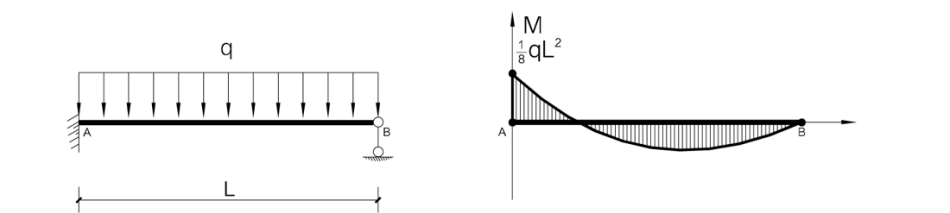
固定端弯矩1/8qL²
类似这种一端固定、另一端简单支承的梁的挠度大小,一般都介于两端固定梁和简支梁之间。然而,其固定端的弯矩却出乎意料地大,即相当于简支梁中央部分的弯矩。对这一点我们应该予以充分的关注。
当把弯矩加在简单支承端时,在固定端则只产生一半的弯矩。在需要计算刚架的应力时,这是一个重要的原理。
连续梁(简支梁+悬臂梁)
2.终端加悬臂梁

内力图规律
- 铰支座处,弯矩为零。
- 集中荷载,剪力图为常数,弯矩图为一次函数。
- 均布荷载,剪力图为一次函数,弯矩图为抛物线,抛物线开口方向与荷载方向相反*。
- 集中外力作用处,剪力突变,突变的大小等于集中力大小,突变方向与集中力方向一致;
- 力偶作用处,弯矩图突变,变化的大小的该力偶矩。
* 按照中国惯例,弯矩图一般画在受拉侧,因为钢筋混凝土使用最为广泛,反应钢筋的受拉特征。在钢结构为主的国家,通常画在受压侧,因为钢结构受压侧容易失稳,设计时更为关键。
在受力简图上,以受弯杆件为X轴线,左侧为原点,建立直角坐标体系。按照中国惯例,弯矩图画在受拉一侧,即下部受拉时弯矩规定为负,上部受拉时弯矩规定为正。


[…] 梁结构内力图 Force Diagram 静定结构内力计算(以简支梁为例) 梁结构内力图 Force Diagram […]
[…] 梁结构内力图 Force Diagram of Beams AWhouse | © 版权说明 | 湘ICP备2020023106号-2 目录 […]
[…] 简支梁M=1/8qL² […]
[…] 简支梁M=1/8qL² […]